Walter Rudin’s third edition provides a rigorous base in analysis, designed for advanced undergraduates and initial graduate studies; a PDF version is widely sought.
Historical Context and Author
Walter Rudin, a prominent 20th-century mathematician, penned “Principles of Mathematical Analysis,” initially published in 1957. This work emerged during a period solidifying the standards for mathematical rigor, building upon the foundations laid by Cauchy, Weierstrass, and Dedekind. Rudin aimed to present a comprehensive and concise treatment of real analysis, distinct from the more intuitive approaches prevalent at the time.
The book quickly became a standard text for advanced undergraduate and beginning graduate courses, renowned for its challenging exercises and precise definitions. Its enduring influence stems from its commitment to logical structure and its coverage of essential topics. Finding a readily available PDF version has become a common pursuit for students globally, reflecting the book’s continued relevance and widespread adoption in mathematical curricula. Rudin’s legacy continues through this influential text.
Target Audience and Prerequisites
“Principles of Mathematical Analysis” is primarily intended for advanced undergraduate students in mathematics, and those beginning their graduate studies. A solid foundation in calculus – including a firm grasp of limits, derivatives, and integrals – is essential. Familiarity with basic set theory and proof techniques is also crucial, as the book emphasizes rigorous mathematical reasoning from the outset.
Students should be comfortable with abstract thinking and prepared for a demanding workload. While not strictly required, prior exposure to real numbers and their properties will be beneficial. Many students seek a PDF version to facilitate study, but possessing the necessary mathematical maturity is more important than simply having access to the text. The book’s exercises require significant effort and independent problem-solving skills.

Core Concepts in Mathematical Analysis
Rudin’s text systematically develops real number systems, sequences, series, limits, and continuity – foundational elements for advanced mathematical exploration, often accessed via PDF.
Real Number System
Rudin’s treatment of the real number system is exceptionally rigorous, beginning with a precise axiomatic foundation. He meticulously constructs the real numbers from the rational numbers, utilizing Dedekind cuts – a method ensuring completeness and avoiding logical gaps. This approach isn’t merely about defining real numbers; it’s about understanding how they are built, emphasizing the inherent properties arising from this construction.
The text delves into the ordering of real numbers, exploring properties like density and the least upper bound property, crucial for subsequent analysis. A key aspect is the focus on proving these properties directly from the axioms, fostering a deep understanding rather than accepting them as given. Students often seek a PDF version to closely follow these detailed proofs and appreciate the logical structure. This foundational chapter is essential, as all further concepts in the book rely heavily on a solid grasp of the real number system’s properties.
Sequences and Series
Rudin’s exploration of sequences and series is characterized by its precision and depth. He begins with the fundamental definitions of convergence and divergence, then systematically builds upon these concepts. A significant portion is dedicated to tests for convergence – ratio, root, comparison, and integral tests – each rigorously proven. He doesn’t simply present the tests; he explains the underlying principles that make them work, demanding a thorough understanding from the reader.
The treatment of series is equally meticulous, covering absolute and conditional convergence, rearrangement theorems, and uniform convergence. Many students utilize a PDF copy of the text to carefully work through the challenging exercises, which are integral to mastering these concepts. Rudin emphasizes the importance of understanding the subtle differences between various types of convergence and their implications. This section forms a cornerstone for understanding more advanced topics like function spaces.

Limits and Continuity
Rudin’s treatment of limits and continuity is foundational, establishing a rigorous framework for the entire subject of mathematical analysis. He meticulously defines limits of functions and sequences, emphasizing the epsilon-delta definition and its implications. Continuity is then defined in terms of limits, leading to a comprehensive exploration of its properties. A readily available PDF version of “Principles of Mathematical Analysis” allows students to closely follow his detailed proofs.
He delves into theorems concerning continuous functions – the Intermediate Value Theorem and the Extreme Value Theorem – providing both proofs and illustrative examples. Rudin doesn’t shy away from challenging exercises designed to test a student’s grasp of these concepts. Understanding these foundational ideas is crucial, as they underpin much of the subsequent material. The book’s clarity, even in its rigor, makes it a valuable resource for self-study and formal coursework.

Fundamental Theorems
Rudin’s text presents pivotal theorems – Intermediate Value, Extreme Value, and Mean Value – with precise proofs; a PDF copy aids detailed study.
The Intermediate Value Theorem
Rudin’s presentation of the Intermediate Value Theorem (IVT) exemplifies his rigorous approach. The theorem states that if f is a continuous function on the closed interval [a, b], and k is any number between f(a) and f(b), then there exists a number c in [a, b] such that f(c) = k.
This seemingly intuitive result is foundational for understanding continuous functions and their properties. Rudin meticulously builds the necessary groundwork for the proof, emphasizing the importance of completeness of the real number system. A PDF version of “Principles of Mathematical Analysis” allows for close examination of the proof’s construction, highlighting the careful use of definitions and logical deductions. Understanding the IVT is crucial not only for its direct applications but also as a stepping stone to more advanced concepts in analysis, such as root-finding algorithms and the existence of solutions to equations.

The Extreme Value Theorem
Rudin’s treatment of the Extreme Value Theorem (EVT) showcases the power of compactness in real analysis. The EVT asserts that if a function f is continuous on a closed and bounded interval [a, b], then f attains both a maximum and a minimum value on that interval. This means there exist points c and d in [a, b] such that f(c) ≤ f(x) ≤ f(d) for all x in [a, b].
The proof, detailed in a PDF copy of “Principles of Mathematical Analysis”, relies heavily on the completeness of the real numbers and the Bolzano-Weierstrass theorem. The EVT is vital for optimization problems and has significant implications in various fields. Rudin’s precise exposition clarifies the crucial role of the closed and bounded interval; continuity alone is insufficient. Mastering this theorem provides a strong foundation for further study in calculus and related disciplines.
The Mean Value Theorem
Rudin’s presentation of the Mean Value Theorem (MVT) in “Principles of Mathematical Analysis” is characteristically rigorous. The MVT states that if a function f is continuous on [a, b] and differentiable on (a, b), then there exists a point c in (a, b) such that f’(c) = (f(b) ⎻ f(a)) / (b ⎼ a). This theorem connects the average rate of change of a function over an interval to its instantaneous rate of change at some point within that interval.
A PDF version of the text reveals Rudin’s emphasis on the necessary conditions – continuity and differentiability are both crucial. The MVT is foundational for many results in calculus, including the proof of Taylor’s theorem. Understanding its proof, which utilizes auxiliary functions, is essential. It’s a cornerstone for analyzing function behavior and solving related problems, demonstrating the power of analytical thinking.

Advanced Topics Covered
Rudin’s text, often found as a PDF, delves into differentiation, Riemann-Stieltjes integrals, and sequences/series of functions, building analytical prowess.
Differentiation
Rudin’s treatment of differentiation in “Principles of Mathematical Analysis,” frequently accessed as a PDF, is exceptionally rigorous. He meticulously builds the theory from first principles, starting with the definition of the derivative as a limit. This approach emphasizes a deep understanding of the underlying concepts, rather than relying on intuitive notions.
The text explores various properties of differentiable functions, including the chain rule, the mean value theorem (covered elsewhere, but foundational here), and Taylor’s theorem. Rudin doesn’t shy away from challenging proofs, demanding careful attention to detail from the reader. He also covers higher-order derivatives and their properties, providing a comprehensive foundation for further study.
A key aspect is the emphasis on the relationship between continuity and differentiability; Rudin demonstrates that differentiability implies continuity, but the converse is not necessarily true. This nuanced understanding is crucial for advanced mathematical work. The PDF version allows for detailed study and annotation of these complex concepts.
Integration (Riemann-Stieltjes Integral)
Rudin’s “Principles of Mathematical Analysis,” often consulted in PDF format, presents a sophisticated treatment of integration, extending beyond the standard Riemann integral to the more general Riemann-Stieltjes integral. This generalization allows integration with respect to functions of bounded variation, offering greater flexibility and power.
He meticulously constructs the theory, starting with the definition of the Riemann-Stieltjes integral and establishing its fundamental properties. Rudin explores the relationship between the Riemann and Riemann-Stieltjes integrals, demonstrating when they coincide. The text delves into theorems concerning integration by parts and change of variables, crucial for advanced applications.
A significant focus is on the existence and uniqueness of the Riemann-Stieltjes integral under various conditions. The PDF version facilitates close examination of the proofs, which require a solid grasp of real analysis concepts. This section provides a strong foundation for further study in measure theory and functional analysis.
Sequences and Series of Functions
Rudin’s “Principles of Mathematical Analysis,” readily available as a PDF, dedicates substantial coverage to sequences and series of functions, a cornerstone of advanced mathematical analysis. This section builds upon the foundation of sequences and series of real numbers, extending these concepts to function spaces.
The text rigorously examines pointwise and uniform convergence, highlighting the crucial differences and implications of each. Rudin presents key theorems, such as the Weierstrass M-test, providing powerful tools for establishing uniform convergence. He explores the interchange of limits and integration/differentiation, conditions under which these operations are valid.
Detailed proofs and examples within the PDF illustrate the subtleties involved; The discussion extends to power series, Fourier series, and other important classes of function series, preparing students for applications in differential equations and complex analysis. A thorough understanding of this material is vital for further mathematical pursuits.
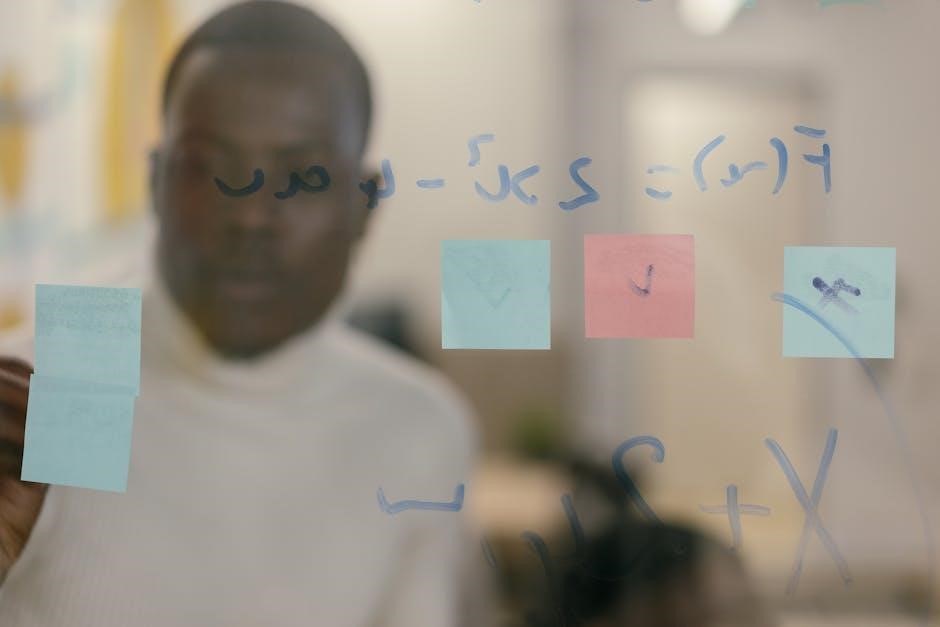
Applications and Relevance
Rudin’s text, often accessed as a PDF, is crucial for the GATE Mathematics syllabus and forms a solid base for Functional Analysis studies.
GATE Mathematics Syllabus Coverage
Walter Rudin’s “Principles of Mathematical Analysis,” frequently studied via PDF versions, demonstrates significant overlap with the Graduate Aptitude Test in Engineering (GATE) Mathematics (MA) syllabus. Specifically, the core concepts detailed within the book – encompassing Calculus, Real Analysis, and Linear Algebra – are foundational elements assessed in the GATE exam.
The syllabus, as outlined for both the 2025 and anticipated 2026 examinations, heavily emphasizes a strong grasp of these analytical principles. Topics like limits, continuity, differentiation, integration, and sequences & series, all meticulously covered by Rudin, constitute a substantial portion of the questions. Furthermore, the book’s treatment of more advanced areas, such as Functional Analysis, provides a valuable stepping stone for tackling related GATE questions.
Therefore, diligent study of Rudin’s text, even in PDF format, serves as an excellent preparation strategy for candidates aiming to excel in the mathematical sections of the GATE examination, building a robust understanding of the underlying theoretical framework.
Foundation for Further Study (Functional Analysis)
Walter Rudin’s “Principles of Mathematical Analysis,” often accessed as a PDF, lays a crucial groundwork for advanced mathematical disciplines, notably Functional Analysis. The rigorous treatment of real number systems, sequences, series, limits, and continuity within the text establishes the necessary analytical maturity.
Functional Analysis builds directly upon these foundational concepts, extending them to infinite-dimensional vector spaces and operators. Rudin’s detailed exploration of these preliminary ideas provides students with the essential tools to navigate the abstract nature of functional spaces like Banach and Hilbert spaces.
Understanding the concepts presented in the book – even through a PDF copy – is paramount for successfully engaging with the more sophisticated theorems and applications encountered in Functional Analysis. It fosters a deep appreciation for mathematical rigor and proof techniques, vital for advanced study and research.

Resources and Supplements
Numerous online forums and readily available PDF solutions manuals complement Rudin’s text, aiding comprehension and problem-solving for students globally.

Solutions Manuals and Online Forums
Navigating Rudin’s “Principles of Mathematical Analysis” often necessitates supplemental resources. While an official solutions manual isn’t directly provided by the publisher, several unofficial solutions manuals, often available as PDF downloads, circulate among students. These can be invaluable for checking work and understanding challenging proofs.
However, reliance solely on solutions manuals should be approached cautiously; the true learning comes from attempting problems independently first. Online forums, such as those found on platforms like GitHub (contributions to projects like enilsen16/The-Math-Group demonstrate active communities), and dedicated mathematics Stack Exchange sites, offer vibrant spaces for discussion.

Students can pose questions, share insights, and collaborate on solutions. These forums provide a supportive environment for tackling the book’s demanding exercises and deepening understanding of the core concepts. Remember to actively participate and contribute to the community, fostering a collaborative learning experience.
